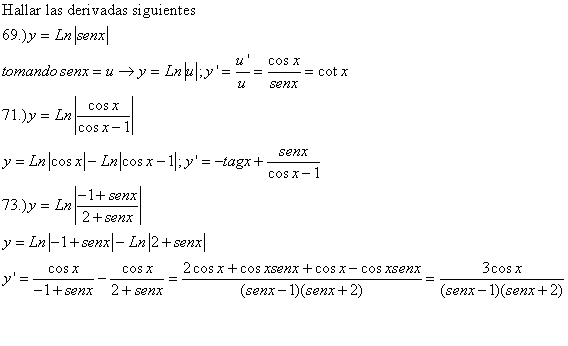Tema 4 Aplicaciones de la derivada. Sección 3.3 Ejercicios 17 a 41 impares

Simulacro Prueba Objetiva Calificable 29/11/2012

Esta prueba es un simulacro de lo que nos podemos encontrar en la Prueba Objetiva Calificable del 11 de Diciembre de 2012. Son cinco preguntas con tres respuestas alternativas. Las preguntas las he sacado de diversos exámenes de selectividad y que corresponden con los cuatro primeros temas de Matemáticas I del Grado de Ciencias Ambientales de la UNED. El sábado 1 de diciembre colgaré las soluciones y desarrollo de todos los ejercicios. Si alguno/a quiere comprobar sus soluciones antes del sábado me lo puede decir o bien haciendo un comentario en esta entrada o por mensaje en facebook http://www.facebook.com/groups/matesCCAA/ o email:  jdomingue638@alumno.uned.es

Tema 4 Aplicaciones de la derivada. Sección 3.1 Ejercicios 37,39,61 y 63

Tema 2 Limites y Continuidad Sección 1.3 Ejercicios 74 y 76

Limite ∞ - ∞

Indeterminación del tipo ∞ - ∞, que se resuelve multiplicando y dividiendo por el conjugado de la expresión algebraica inicial.

Tema 4. Aplicaciones de la derivada. Sección 3.1 ejercicios 11 a 35 impares

En los ejercicios 11, 13 y 15, se trata de hallar los puntos críticos en el intervalo indicado. Para eso tenemos que recordar las condiciones que se tienen que dar para que haya un punto critico en  c,  dichas condiciones son:
1. La función tiene que estar definida en c
2. La derivada de la función en c vale 0, f '(c)=0, ó no existe la derivada en ese punto

En los ejercicios del 17 al 35, hay que hallar los extremos absolutos de la función en el intervalo dado. Para eso tenemos que evaluar la función en los puntos terminales  del intervalo y en aquellos puntos críticos que tenga la función en el intervalo dado.

Tema 3. Derivación Sección 5.6 Ejercicios 43 a 61 Impares

NUEVA PUBLICACIÓN, CORRECCIÓN  EJERCICIO 59 GRACIAS A LA COLABORACIÓN DE ANTONIO REPULLO

Tema 3 Derivación. Sección 2.1 ejercicio 24

NUEVA PUBLICACIÓN DE ESTE EJERCICIO TRAS CORREGIR UN ERROR. GRACIAS
A LA COLABORACIÓN DE JOSÉ LUIS CEBALLOS MORENO.

Cálculo de una derivada aplicando la definición. Evidentemente este método es mucho más tortuoso que aplicar la regla de derivación correspondiente, pero no deja de tener su encanto....

Tema 1 Preliminares Sección P3 ejercicios 16, 38, 45 y 75

Una recopilación de ejercicios resueltos en el foro de Matemáticas I de la UNED (curso 2012-2013) 

Ejercicio 16

Ejercicio 38 RESUELTO POR LUIS TAMARGO

Ejercicio 45

Ejercicio 75

Tema 3. Derivación Sección 2.4 Ejercicios 111 y 115

Dos típicos problemas donde nos dan la función y al derivarla obtenemos la razón de cambio

Tema 3. Derivación. Sección 5.5 Ejercicios 41 a 61 impares

Ejercicios de derivación de funciones exponenciales y logarítmicas.  Conviene en algunas funciones hacer transformaciones mediante las propiedades de los logaritmos para hacer la función más fácil de derivar.

Tema 3 Derivación. Sección 2.4 Ejercicios 7 a 35 y 45 a 65 impares

Tema 3 Derivación. Sección 2.3. Ejercicios 93,95,97,99, 101 y 107

Tema 3. Derivación Sección 2.3 Ejercicios 73,75,79,83,85 y 87

Tema 3. Sección 5.4 Ejercicios 39 a 59 Impares

Tema 3 Derivación Sección 5.1 Ejercicios 47 a 73 impares

Ejercicio 67

Tema 3 Derivación Sección 2.3 ejercicios 73,75,79,83,85 y 87

Tema 3 Derivación Sección 2.2 Ejercicios 59,61 y 63

Tema 3 Derivación Sección 2.3 ejercicios 25 a 53 solo impares

Tema 3 Derivación Sección 2.2 ejercicios 65, 67, 69 y 81

Tema 3 Derivación Sección 2.2 ejercicios 3 a 24, 31 a 38 y 39 a 54 Todos impares

Tema 2 Límite y Continuidad Sección 1_4 ejercicios 107 y 109

107.) Un sábado a las 8:00 de la mañana, un hombre comienza a subir corriendo la ladera de una montaña hacia su camping de fin de semana. El domingo a las 8:00 de la mañana baja corriendo la montaña. Tarda 20 minutos en subir y sólo 10 en bajar. En cierto punto del camino de bajada, el hombre se da cuenta que pasó por el mismo lugar a la misma hora al sábado. Demostrar que el hombre está en lo cierto. Sugerencia: Considerar que s(t) y r(t) son las funciones de posición de subida y bajada y aplicar el teorema del valor intermedio a la función f(t)=s(t)-r(t).

Como el hombre tarda 20 minutos en subir y 10 minutos en bajar, si hay algún punto de coincidencia tiene que ser en un intervalo de 10 minutos como máximo, por tanto considero el intervalo a estudiar [0,10].

Como el teorema del valor intermedio nos garantiza al menos un cero (en este caso el cero es el punto de coincidencia) siempre que f(a) tenga signo distinto que f(b) en un intervalo [a,b], por tanto tenemos que probar que f(0) tenga diferente signo a f(10).

como f(t)=s(t)-r(t)

f(0)=s(0)-r(0)=0-r(0) por lo que -r(0) <0. 

s(0) es cuando el hombre el sábado no ha empezado a subir, por tanto no recorre nada y la función vale cero.

 r(0) es cuando el hombre el domingo está arriba de la colina, no ha empezado a bajar pero la función si tiene un valor que es la altura a la que se encuentra, por eso -r(0) es negativo.

f(10)=s(10)-r(10)=s(10)+0 por lo que s(10)>0

s(10) es cuando el hombre el sábado lleva recorrido cierto espacio y por tanto la función tiene un valor

 r(10) es cuando el hombre el domingo ha llegado a la base de la colina y por tanto r(10)=0

Como f(0) tiene signo distinto de f(10) entonces el hombre lleva razón en su apreciación.

109.) Demostrar que si f es continua y carece de ceros en [a,b] entonces

F(x)>0 para todo x en  [a,b] o f(x)<0 para todo x en  [a,b].

Una forma de demostrar lo que piden es la siguiente. Si f no tuviera signo constante en [a,b] entonces habría dos puntos c y d (c < d, por ejemplo) en los que f tendría signo distinto. Pongamos, por ejemplo, f(c) < 0 < f(d). Resultaría entonces que en el intervalo [c,d] la función f, que es continua, cambiaría de signo. Por el teorema de los valores intermedios (tal y como tú lo aplicas en el 107), f tendría un cero en [c,d]. Pero esto es falso por hipótesis. 

Ejercicio resuelto por: Francisco Javier Cirre Torres (Coordinador de la asignatura Matemáticas I

Tema 2 Límite y Continuidad Sección 1.4 ejercicios 83,85,91 y 93

Tema 2 Límites y Continuidad Sección 1.4 ejercicios 63, 65 y 67

Tema 2 Límite y Continuidad Sección 1.4 ejercicios 35 a 57 (impares)